Spenning
Spenning med symbol $v$ (noen ganger på norsk $u$) mellom to punkter forteller noe om hvor mye energi som må brukes til å flytte en +ladning fra punktet med lavest potensial opp til punktet med høyest potensial. Motsatt; når en ladning slippes fra punktet med høyest potensial ned til punktet med lavest potensial frigjøres energi.
Legg merke til at vi bruker ordet potensial mye i sammenheng med spenning. Spenning er potensialforskjellen mellom to punkter. Spenning kalles også noen ganger elektromotorisk kraft eller elektromotorisk potensial.
Spenning måles i volt ($\mathrm{V}$) og vi måler som regel spenning i områder fra $1\mathrm{mV}$ til noen $\mathrm{kV}$.
Spenning defineres ut fra ladningens størrelse og arbeidet som gjøres for å flytte ladning mellom to punkter.

Spenningen ligger over komponenten. Spenningen markeres med $+$ der potensialet er høyest og $-$ der potensialet er lavest.
Strøm
Strøm med symbol $i$ er et mål på hvor raskt ladning passerer gjennom et punkt.
Strøm har enheten Ampere ($\mathrm{A}$). Vi måler som regel strøm i størrelser fra $1\mu\mathrm{A}$ opp til noen $\mathrm{A}$, men i noen tilfeller også så små strømmer som $\mathrm{nA}$ og til og med $\mathrm{pA}$.

Strøm går gjennom en komponent. Strøm markeres med en pil i den retning positiv ladning beveger seg.
Strøm i elektronikken er elektroner som forflytter seg. Disse er negativt ladede. De beveger seg mot strømretningen.
Elektriske kretser
Når vi kobler sammen komponenter med ledninger lager vi elektriske kretser. Vi regner spenningen over en ledning som null. Strømmen gjennom en ledning er som regel ulik null.
For hver komponent i en slik krets går det strøm gjennom komponenten, mens det ligger en spenning over komponenten.
Når flere enn to ledninger er koblet til samme punkt kaller vi dette en node.
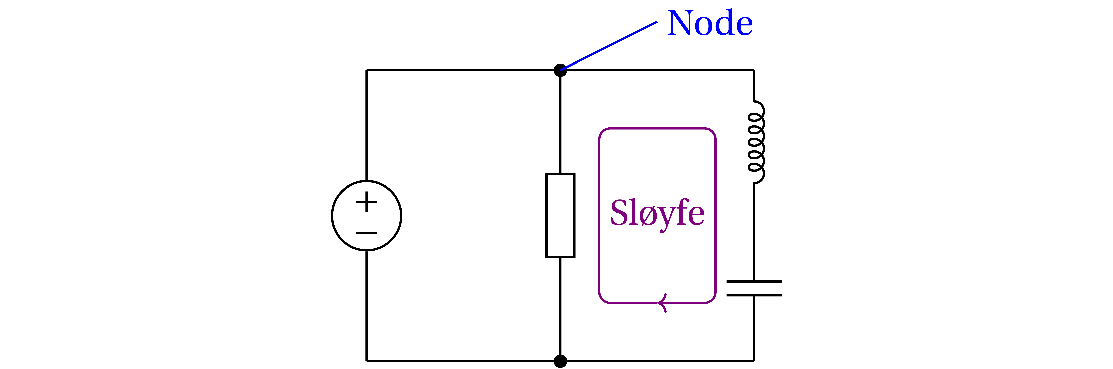
En vei gjennom en krets som starter og slutter i samme node (og ikke krysser seg selv) kalles en sløyfe.
Eksempel:
Kretsen over har
- To noder: En oppe og en nede. Som markert med en hvit prikk.
- Tre sløyfer: en til høyre i kretsen (slik som tegnet inn), en til venstre i kretsen og en rundt hele kretsen.
Det er spenningsforskjell mellom nodene. Strøm går gjennom sløyfene.
Effekt
Effekt mottatt av et kretselement er
$
p = v \cdot i
$
og måles i watt ($\mathrm{W}$).
Effekt blir vanligvis til varme i en komponent. Effekten er positiv når en komponent mottar effekt, slik som i en lyspære. Effekten er negativ når den leveres av en komponent, slik som for et batteri. Dette kalles passiv fortegnskonvensjon.
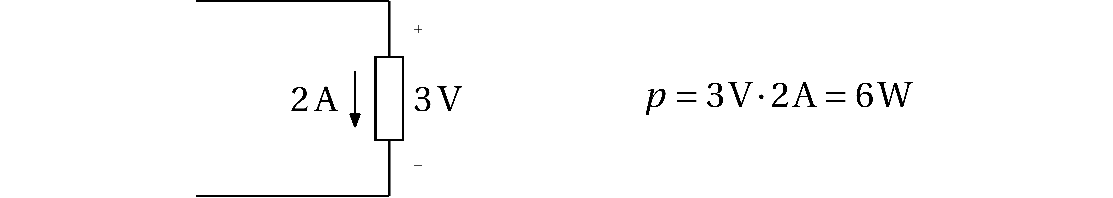
Spenningslov
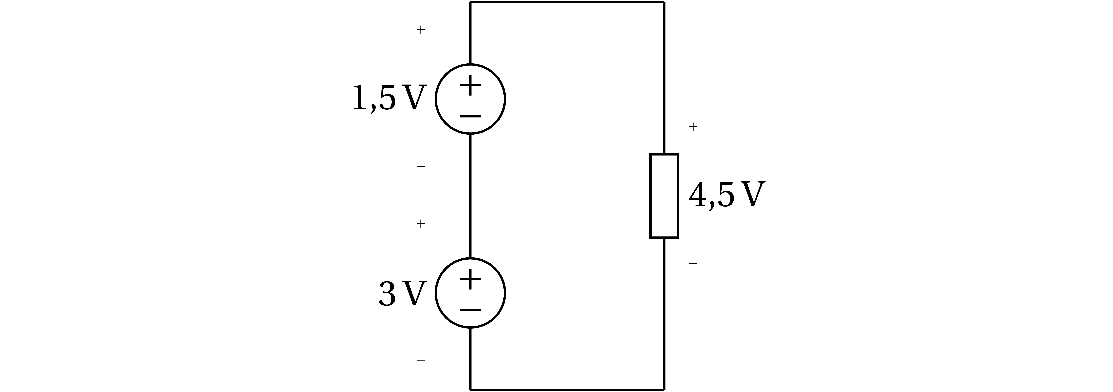
Summen av alle spenningsstigninger er like summen av alle spenningsfall i en sløyfe.
For eksempel, dersom vi seriekobler to batterier med spenningsstigning på $3\mathrm{V}$ og $1,5\mathrm{V}$ og kobler disse til en lyspære så vil spenningsfallet over lyspæren være $3\mathrm{V}+1,5\mathrm{V} = 4,5\mathrm{V}$.
 Denne loven kalles Kirchhoffs spenningslov, eller Kirchhoffs andre lov.
Denne loven kalles Kirchhoffs spenningslov, eller Kirchhoffs andre lov.
Et viktig resultat: To komponenter i parallell har alltid samme spenning.
Strømlov
All strøm som kommer inn mot et punkt må også gå ut av samme punkt.
For eksempel, dersom to ledere sender strøm inn mot et punkt på $1\mathrm{A}$ og $1,5\mathrm{A}$ og det er en tredje leder tilkoblet punktet må strømmen gå ut gjennom denne lederen. Og strømmen ut blir:
$$1\mathrm{A} + 1,5\mathrm{A} = 2,5\mathrm{A}$$
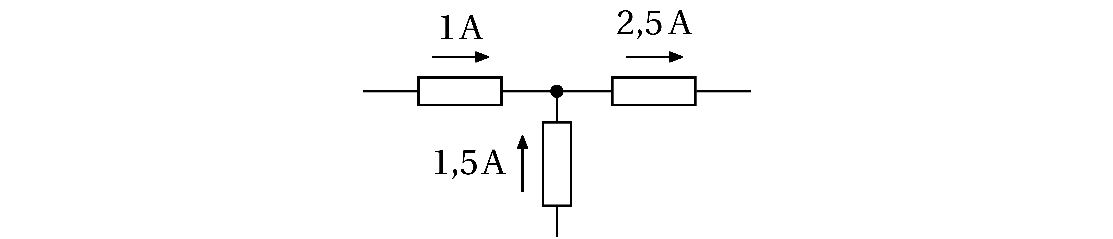
Denne loven kalles Kirchhoffs strømlov, eller Kirchhoffs første lov.
Et viktig resultat: To komponenter i serie har alltid samme strøm.
iv-karakteristikk
Elektronikk handler aller mest om å utnytte komponenter som har ulike former for sammenheng mellom strøm $i$ og spenning $v$. Dette er så sentralt at vi trenger å kjenne komponenters $iv$-karakteristikk. Dette er rett og slett et plott (en kurve) der vi tegner strøm som funksjon av spenning. Med andre ord strøm på den vertikale aksen, og spenning langs den horisontale.
Vi kan ha svært enkle slike plot
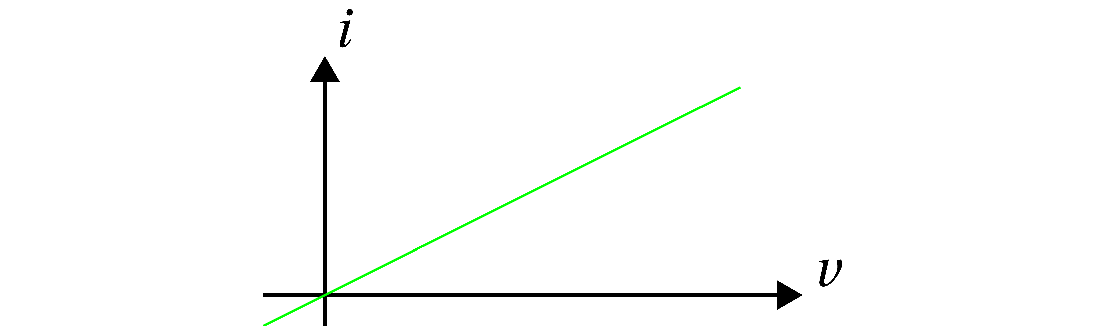
der sammenhengen er lineær slik som for en motstand.
Eller litt mer kompliserte og til og med sammensatte slike plot. For eksempel er sammenhengen eksponensiell for dioder:
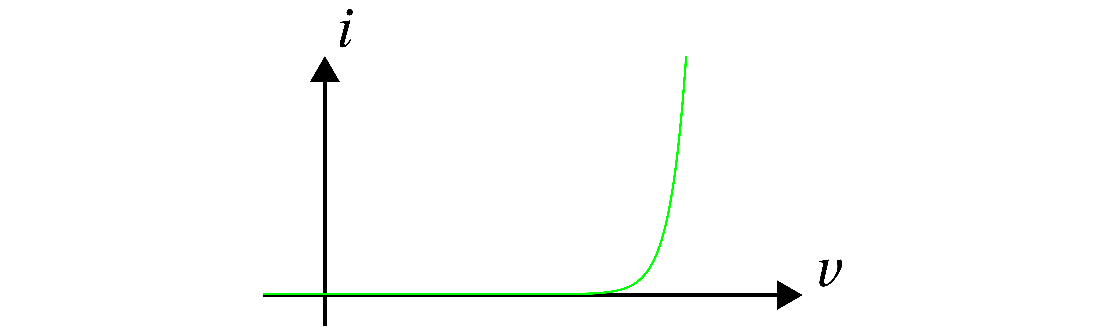
Vi bruker $iv$-karakteristikk for å introdusere ulike komponenter (der det er naturlig).
Strømkilde
Strømkilder er litt vanskelige å se for seg. Som regel lager vi dem med andre komponenter som for eksempel transistorer. Det kan være nyttig å huske på at et batteri er ikke en strømkilde, men en spenningskilde.
I alle tilfeller teger vi den med en sirkel og en pil som viser hvilken vei strømmen går:

Det er viktig å huske at det eneste vi vet om en strømkilde er strømmen den kan levere. Spenningen over den er ukjent helt til vi kobler kilden til en krets. Dette markerer vi i $iv$-karakteristikken ved å tegne strømmen som en konstant, men legg merke til at alle mulige spenninger kan ligge over kilden.
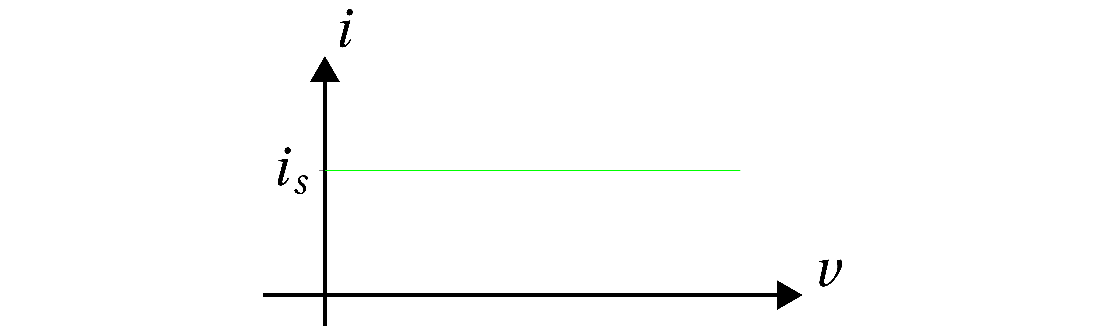
Strømkilder kan som spenningskilder være konstante eller variere:
- konstant over tid: likestrøm også kalt dc-strøm.
- variere i et repeterende mønster over tid: vekselstrøm også kalt ac-strøm
Spenningskilde
En spenningskilde kan være for eksempel et batteri, forsyningen til en laptop, eller rett og slett en stikkontakt. I alle tilfeller teger vi den med en sirkel og en $+$ og en $-$ som viser hvilken vei spenningen stiger:

Det er viktig å huske at det eneste vi vet om en spenningskilde er spenningen den kan levere. Strømmen gjennom den er ukjent helt til vi kobler kilden til en krets. Dette markerer vi i $iv$-karakteristikken ved å tegne spenningen som en konstant, men legg merke til at alle mulige strømmer kan gå gjennom kilden.
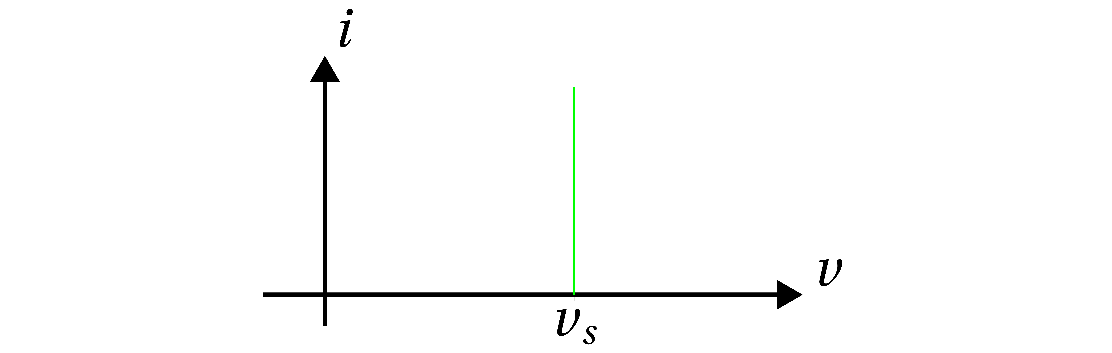
Spenningen kan være
- konstant over tid: likespenning også kalt dc-spenning.
- variere i et repeterende mønster over tid: vekselspenning også kalt ac-spenning
- ha en variasjon over tid som ikke repeteres.
Eksempel på likespenning er et batteri. Stikkontakten gir fra seg en vekselspenning. En sensor (det vil si for eksempel et måleinstrument) kan gi fra seg en tidsvariende spenning.
Motstand
Motstander, eller resistanser, er den vanligste komponenten brukt i kretser og elektronikk. Den følger en svært enkel sammenheng for strøm og spenning. Sammenhengen er gitt av Ohms lov:
$
i = \frac{1}{R}v
$
Dette gir oss $iv$-karakteristikken til en motstand:
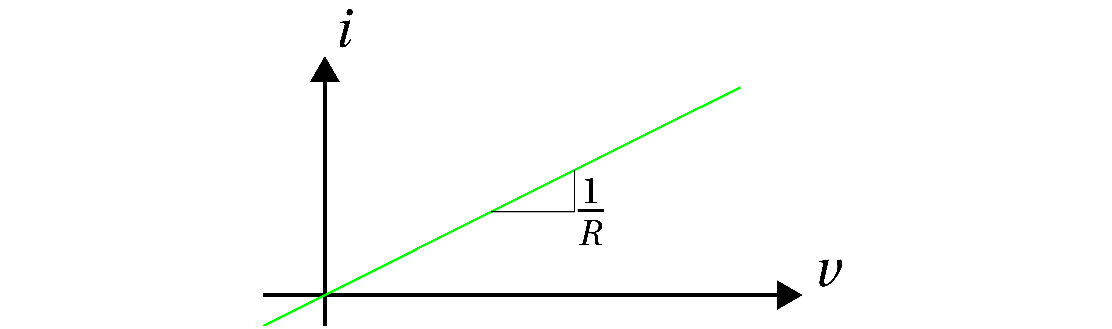
Som vi ser er sammenhengen lineær, den skjærer gjennom origo og stigningstallet til kurven er $\frac{1}{R}$.
$R$ i denne sammenhengen er motstandens resistans. Den måles i Ohm ($\Omega$).
Selve komponenten tegner vi som et enkelt rektangel, med to terminaler. Det finnes en rekke standardverdier for motstander. Overraskende nok er standarverdiene sjelden runde tall.

Her har vi også tegnet med korrekt retning på spenningsfall og strømretning (husk passiv fortegnskonvensjon).
I noen land slik som USA tegnes motstanden gjerne med et sikk-sakk-symbol. Dette er også vanlig i programvare som simulerer elektriske kretser.

Andre komponenter
Vi har selvfølgelig en rekke andre komponenter. Bildet under viser de viktigste.
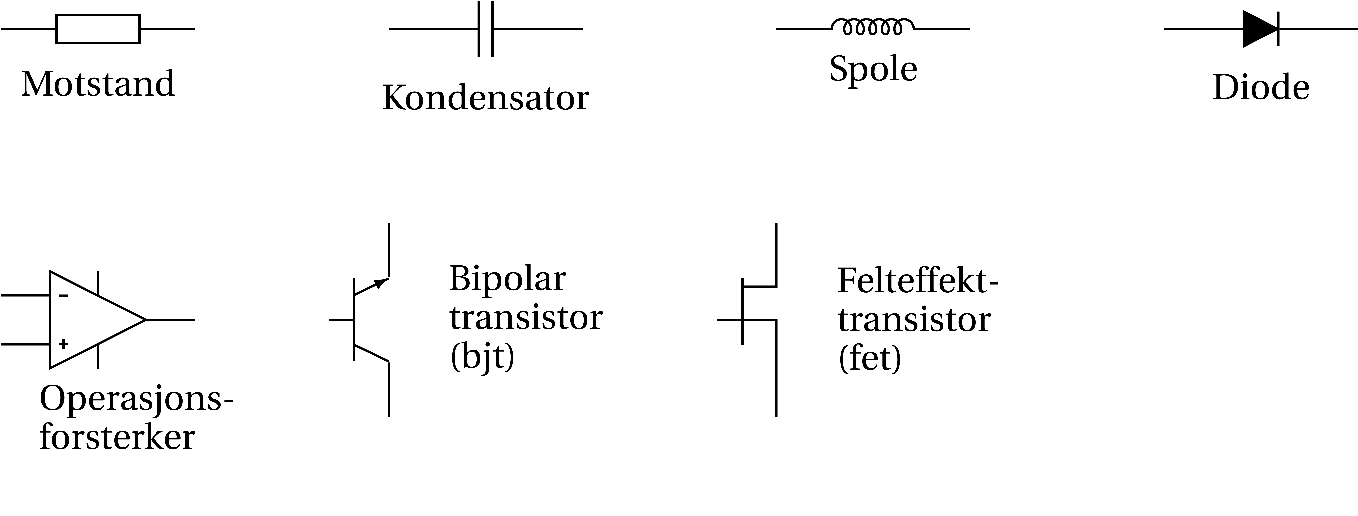
Selvfølgelig finnes det en rekke andre som transformatorer og tyristorer. Komponentene i bildet over finnes i mange spesialutgaver. En motstand kan være variabel. En diode kan gi fra seg lys slik som en lysdiode. Lysdioder kalles gjerne LED (light emitting diode). Felteffekttransistorer finnes i mange utgaver som for eksempel mosfet og jfet.
Men før du lærer om de bør du lese mer om og arbeide med Elektriske kretser og etterhvert også Elektronikk.
Enheter og prefikser
Enheter brukes for at ingeniører, teknologer og forskere skal ``snakke samme språk''. Det internasjonale systemet for enheter, SI (International System of Units), har vært i bruk siden 1960-tallet. Systemet baserer seg på syv grunnstørrelser som andre størrelser kan utledes fra. Tabellen under viser noen av de SI-enheter som er relevante for elektronikkingeniører
| Størrelse |
Enhet |
Kortform |
| Tid |
sekund |
s |
| Elektrisk strøm |
ampere |
A |
| Ladning |
coulomb |
C |
| Spenning |
volt |
V |
| Energi, arbeid |
joule |
J |
| Effekt |
watt |
W |
| Motstand |
ohm |
Ω |
| Kapasitans |
farad |
F |
| Induktans |
henry |
H |
| Frekvens |
hertz |
Hz |
SI har også standardisert prefikser som kan benyttes for å skrive veldig store og veldig små tall. Tabellen neders viser prefikser, med symbol og navn. Ved hjelp av SI-symboler og prefikser kan vi nå skrive for eksempel et tusendels sekund på følgende måter:
$$
\frac{1}{1000}\mathrm{s} = 0.001\mathrm{s} = 1\mathrm{ms} = 1000 000 \mathrm{ns}
$$
| multiplikator |
symbol |
navn |
| $$10^{18}$$ |
$$\mathrm{E}$$ |
exa |
| $$10^{15}$$ |
$$\mathrm{P}$$ |
peta |
| $$10^{12}$$ |
$$\mathrm{T}$$ |
tera |
| $$10^{9}$$ |
$$\mathrm{G}$$ |
giga |
| $$10^{6}$$ |
$$\mathrm{M}$$ |
mega |
| $$10^{3}$$ |
$$\mathrm{k}$$ |
kilo |
| $$10^{2}$$ |
$$\mathrm{h}$$ |
hecto |
| $$10$$ |
$$\mathrm{da}$$ |
deka |
| $$10^{-1}$$ |
$$\mathrm{d}$$ |
deci |
| $$10^{-2}$$ |
$$\mathrm{c}$$ |
centi |
| $$10^{-3}$$ |
$$\mathrm{m}$$ |
milli |
| $$10^{-6}$$ |
$$\mathrm{\mu}$$ |
micro |
| $$10^{-9}$$ |
$$\mathrm{n}$$ |
nano |
| $$10^{-12}$$ |
$$\mathrm{p}$$ |
pico |
| $$10^{-15}$$ |
$$\mathrm{f}$$ |
femto |
| $$10^{-18}$$ |
$$\mathrm{a}$$ |
atto |
Introduksjon
Noen lover og regler (og noen triks) legger grunnlaget for elektronikken. For å lære om elektronikk er det nødvendig å ha alt det grunnleggende helt på plass slik som
og komponenter som deler av elektriske kretser.
Fysikken som gir grunnlag for elektronikken er kompakt og oversiktlig. Men ulikt mye annet er ikke elektrisitet noe vi kan se eller høre. I tillegg er nok terminologien (ordene vi bruker) uvanlige og noen ganger ukjente.
Matematikken som forteller oss hvordan en elektrisk krets virker er viktig. Den inneholder temaer som mange har hørt om, men ikke fått helt grep om. Å lære om Elektronikk er kanskje den beste måten å lære denne matematikken. Har vi forstått fysikken faller matematikken raskt på plass.



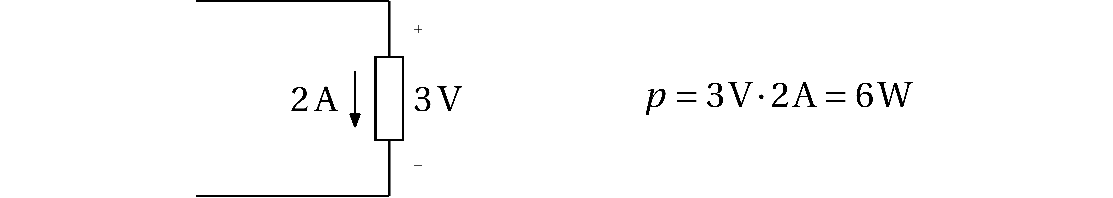
 Denne loven kalles Kirchhoffs spenningslov, eller Kirchhoffs andre lov.
Denne loven kalles Kirchhoffs spenningslov, eller Kirchhoffs andre lov.